Breakout Exercise 1 - Expression Heatmap

Estimated time: 15 Minutes

Motivation

Plotting the expression values across all samples for the top variable genes in an experiment can help to visualize how samples cluster together by their expression profiles. When combined with phenotypic data, it can help show how samples with different treatments behave relative to one another.

Exercise

Create a heatmap of the top 50 most variable genes using the pheatmap() function using the rlog normalized data in the rld object.

Instructions

• One group member should share their screen in the breakout room. If nobody volunteers, a helper may randomly select someone.
• The group members should discuss the exercise and work together to find a solution.
• If there is time after a solution is found, allow all members to complete the exercise.

Example

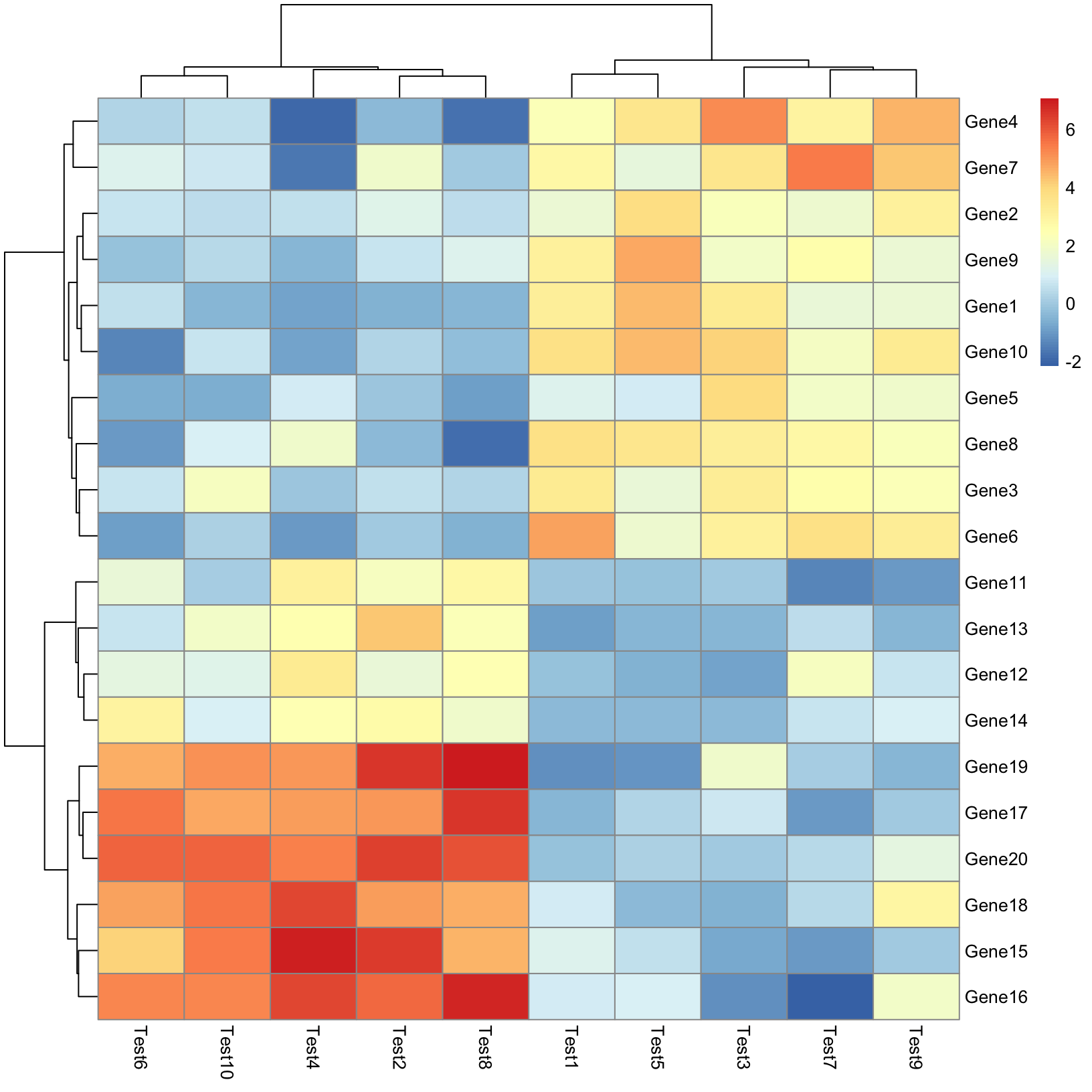
To get an idea of what we expect to see at the end, let’s look at a toy example from the pheatmap() help examples. There’s no need to run this code, we just want to illustrate the form of the result.

# Copied from the pheatmap documentation

# Create matrix with random normally distributed values
test = matrix(rnorm(200), 20, 10)

# Impose some structure so the heatmap appears interesting
test[1:10, seq(1, 10, 2)] = test[1:10, seq(1, 10, 2)] + 3
test[11:20, seq(2, 10, 2)] = test[11:20, seq(2, 10, 2)] + 2
test[15:20, seq(2, 10, 2)] = test[15:20, seq(2, 10, 2)] + 4

# Name the rows and columns
colnames(test) = paste("Test", 1:10, sep = "")
rownames(test) = paste("Gene", 1:20, sep = "")

# Draw the heatmap
pheatmap(test)

Steps

1. Look at the documentation for the pheatmap() function and determine what the most important parameter is. Hint: It’s usually the first or first few parameters. This is telling us what we’ll have to get for the next step.

Answer

?pheatmap

For this exercise, we’ll only need to use the mat parameter, giving the numeric matrix to be plotted.

2. Extract the rlog normalized expression values for the experiment. Hint: We created an rld object earlier. The assay() function pulls out the values.

Answer

exp_mat = assay(rld)
head(exp_mat)

                    sample_A  sample_B  sample_C  sample_D  sample_E  sample_F
ENSMUSG00000000001 10.514813 10.366709 10.419463 10.840373 10.410449 10.578771
ENSMUSG00000000028 10.604461 10.734506 10.735026 10.682714 10.820938 10.990999
ENSMUSG00000000031 11.160276 10.498747 10.742763 11.861617 10.578156 10.298022
ENSMUSG00000000037  4.642433  4.555500  4.578934  4.656950  4.719012  4.620204
ENSMUSG00000000049  3.017478  2.820198  2.843894  2.936455  2.814833  2.811619
ENSMUSG00000000056 14.321672 14.284652 14.337197 13.904238 14.393912 14.235971

3. Calculate the variance for each gene in the expression matrix we just extracted. Hint: Look at the help for matrixStats::rowVars() and decide if that’s a reasonable function to use.

Answer

gene_vars = rowVars(exp_mat)
head(gene_vars)

[1] 0.030341701 0.017700141 0.326567308 0.003409940 0.007135949 0.030863320

4. Get the numerical indices for the top 50 most variable genes. Hint: Run the order() function on a toy example, like order(c(-1.25, 1.3, 5.6, 2.1)), and think about what is being returned. Note, it’s not the values in the original vector. Then look at the help for order() and figure out how how to reverse what is returned.

Answer

order(c(-1.25, 1.3, 5.6, 2.1))

[1] 1 2 4 3

order(c(-1.25, 1.3, 5.6, 2.1), decreasing = TRUE)

[1] 3 4 2 1

ordered_idx = order(gene_vars, decreasing = TRUE)
top_50_idx = ordered_idx[1:50]

5. Subset the expression matrix from step 2 using this index vector. Hint: Remember square-bracket notation, and that we want to subset the rows, while returning all the columns. Make sure the result has the number of rows you expect, that is, 50.

Answer

top_var_exp_mat = exp_mat[top_50_idx, ]
dim(top_var_exp_mat)

[1] 50  6

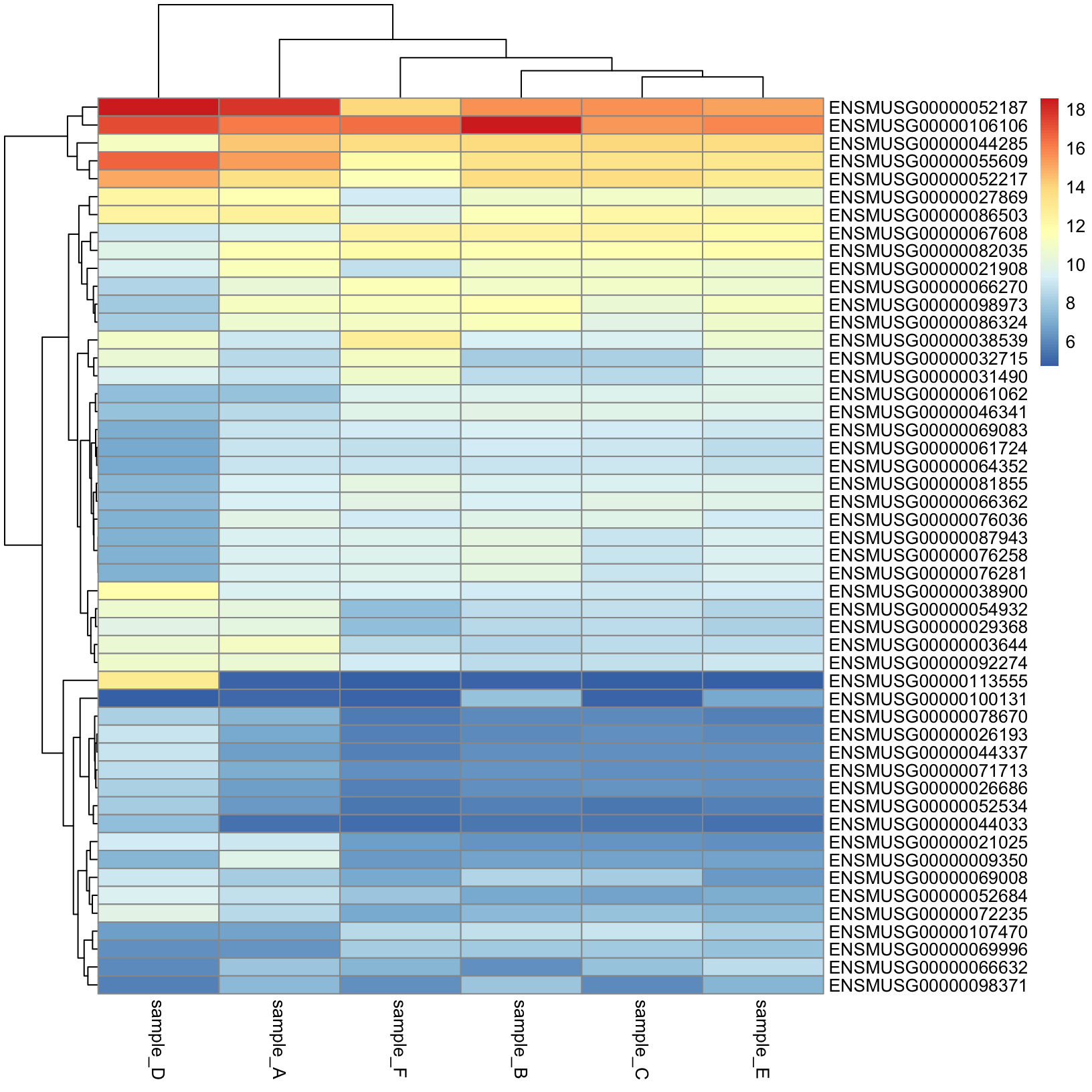
6. Create a heatmap using this subsetted expression matrix using the pheatmap() function.

Answer

pheatmap(top_var_exp_mat)

Saving the result

If time permits, discuss with your group how you might save this heatmap. Hint: Look at the parameters for the function in ?pheatmap. Alternatively, consider how we saved the PCA in the previous module.