Module 09: Sample QC

Objectives

• Generate common QC visualizations
• Understand how to interpret QC visualizations
• Understand when to revise the model used in the DESeq2 initialization
• Understand the pitfalls of post-hoc analysis
• Describe the causes and implications of batch effect or other QC issues in an RNA-Seq experiment

Differential Expression Workflow

Prior to testing for differential expression between our comparisons of interest, we’ll first generate plots that will assess how well our samples match up with our expectations (based on their treatment groups) and what we might expect to see from our differential expression comparisons.

---

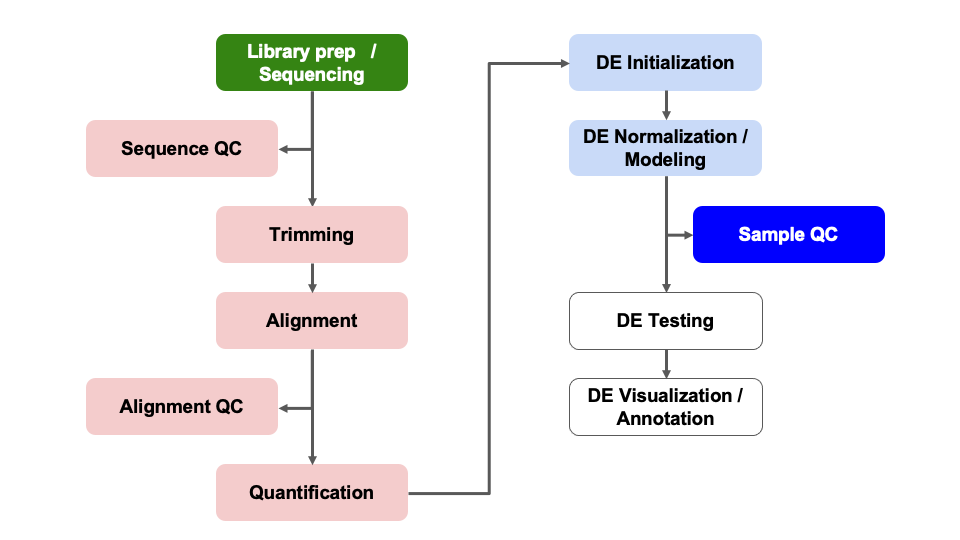
QC Visualizations

We have discussed some aspects of quality control assessment at the sequencing level. Today we will outline sample-level and gene-level quality control assessments to determine what we might expect for our differential expression comparisons.

To do this, we will first assess the similarity of our samples by using principal component analysis (PCA). This will allow us to determine how well patterns in the data fits our expectations from the experiments design and possible sources of variation.

Other common visualizations that we generate for our analyses include expression heatmaps, sample correlation heatmaps, and boxplots of raw and/or normalized counts, the code for which (due to time restrictions) can be found as bonus content through the materials for today and in the bonus content module.

Principal Component Analysis

A common and very useful plot for evaluating how well our samples cluster by treatment groups are Principal Component Analysis (PCA) plots. PCA is used to emphasize variation and bring out patterns in large datasets by using dimensionality redution.

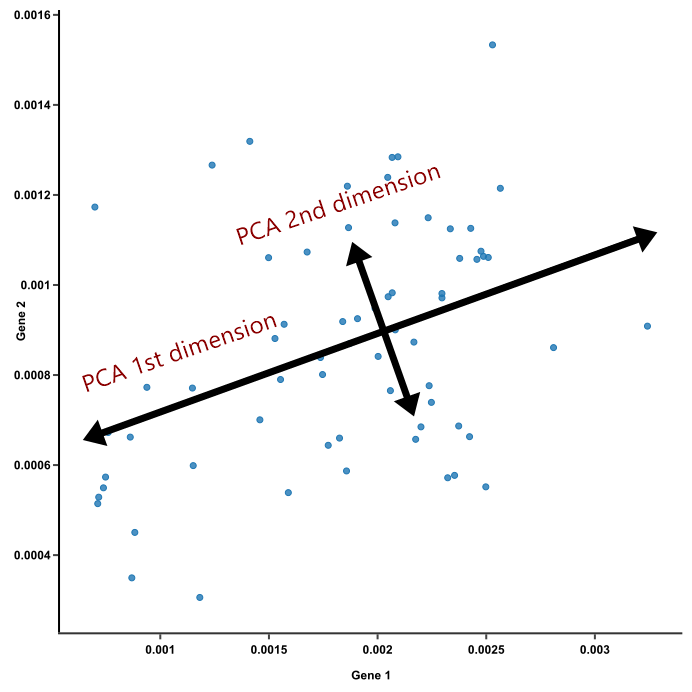
This image from a helpful step by step explaination of PCA helps to illustrate the principal component projections for two genes measured in approximately 60 mouse samples. Generally, this process is repeated and after each gene’s contribution to a principal component or weight is determined, the expression and weight are summed across genes for each sample to calculate a value for each principal component.

Note: A more detailed overview of the PCA procedure is outlined in a Harvard Chan Bioinformatic Core training module and is based on a more thorough description presented in a StatQuest’s video. Additionally, this TowardsDataScience blog post goes through the math behind PCAs.

Interpreting PCA plots

For most bulk RNA-seq experiments, we expect the majority of the total variance to be explained by the first two or three principal components. In the following plot, principal component 1 (PC1) explains ~80% of the variance in our data while principal component 2 (PC2) explains ~12% of the variance, which fits that expections.

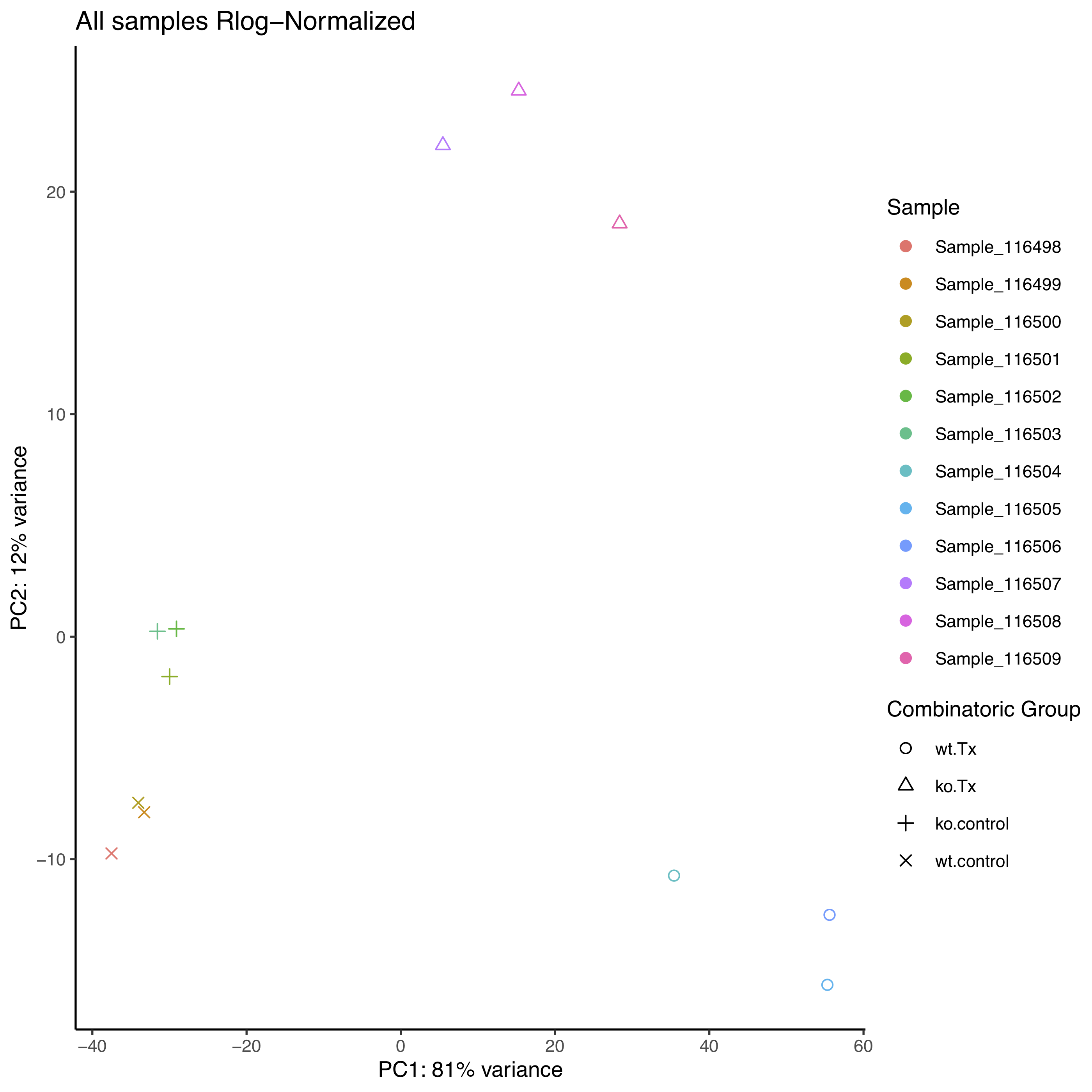
Question

How might we interpret the variance explained by each principal component in the context of the labeled sample points?

For more information, this helpful overview of PCA basics walks through both the generation and interpretation of PCA plots.

Evaluating batch effects or confounders

PCA plots are also useful for evaluating the impact of factors other than the experimental treatment or group. At times, batch effects can be quite obvious, such as this example from the DESeq2 vignette, where samples within each treatment group look staggered into two subgroups.

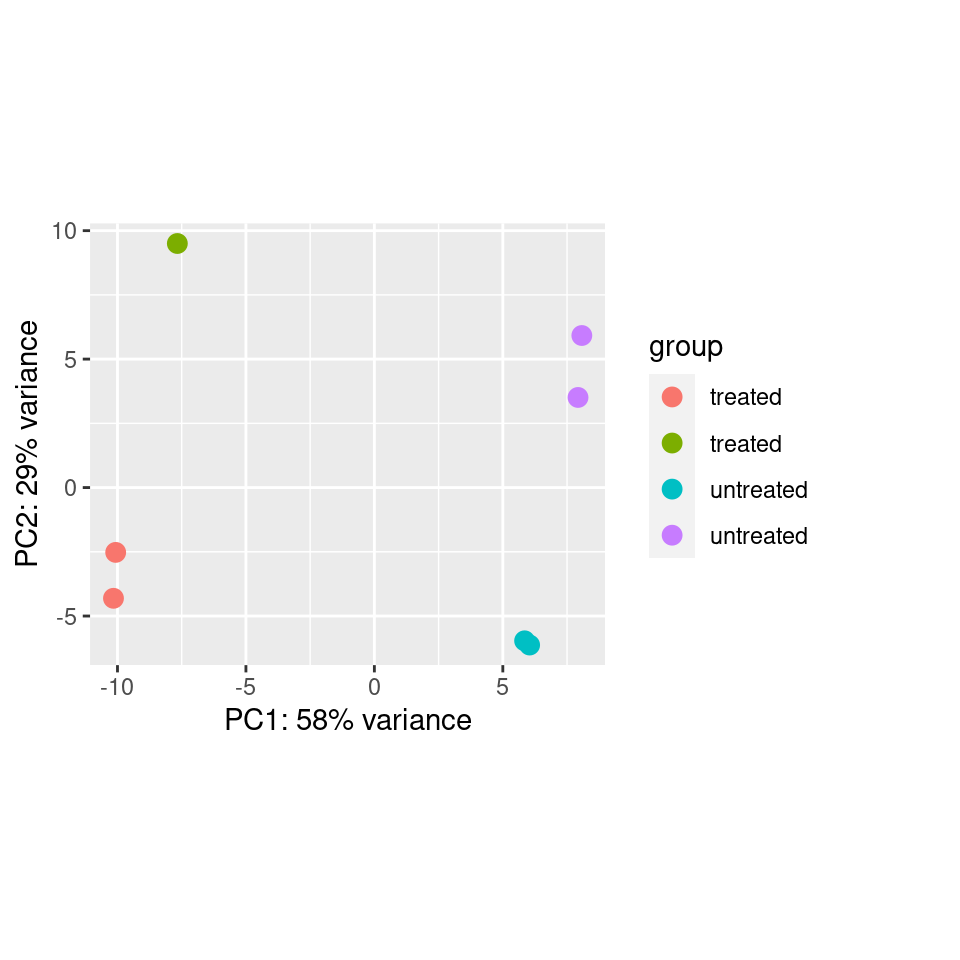
It turns out this experiment contained samples sequenced single-end and paired-end. If we color only by sequencing run type (paired-end vs. single-end), we see that PC2 (29% of variance) is primarily explained by this technical covariate.

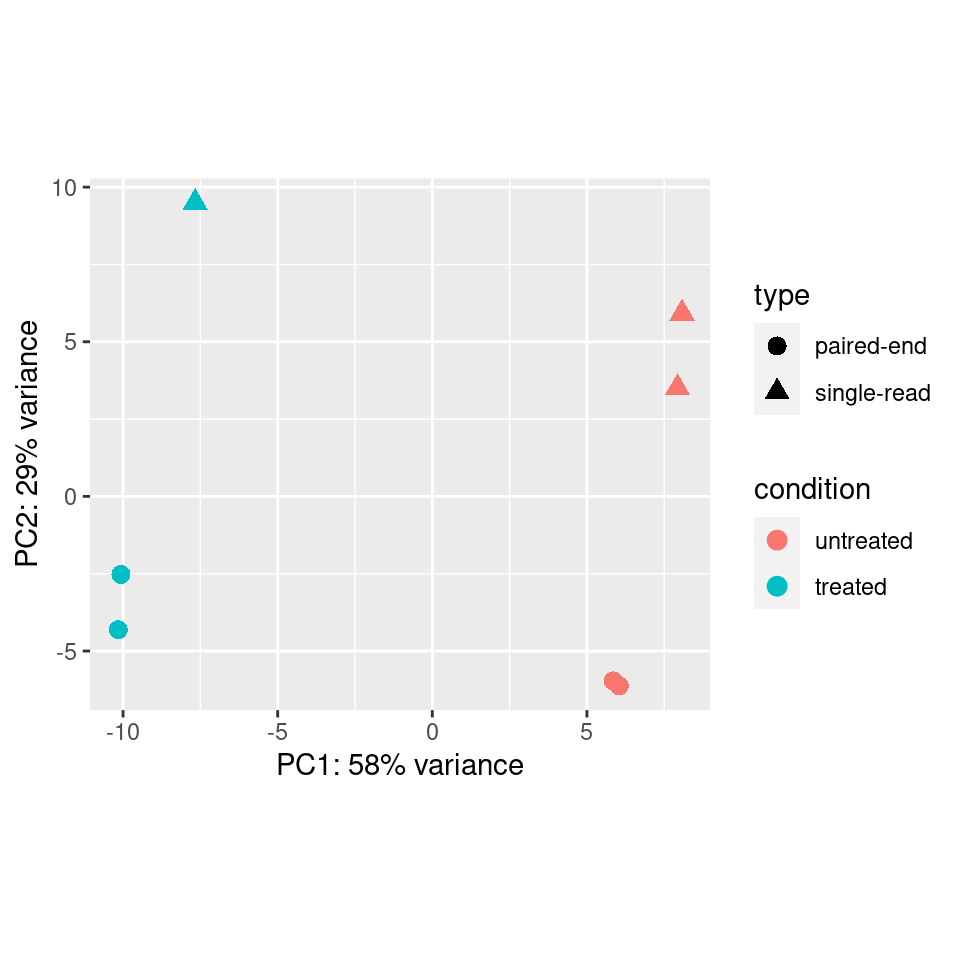
However, the samples are clearly seperated by experimental condition on PC1 and since we have non-confounded batches, if we saw this pattern in our data we could incorporate the technical covariate into our model design, such as outlined in the DESeq2 vignette.

Click for complex design discussion

In experiments with more complex designs, such as when there are interesecting/multiple treatment conditions, it can be less clear what covariants are influencing expression, such as illustrated from this documenation for a microarray analysis tool. From the PCA labeled by experimental treatment, we see that samples from the treatment group do not cluster together and that there is high variance across all treatment groups. 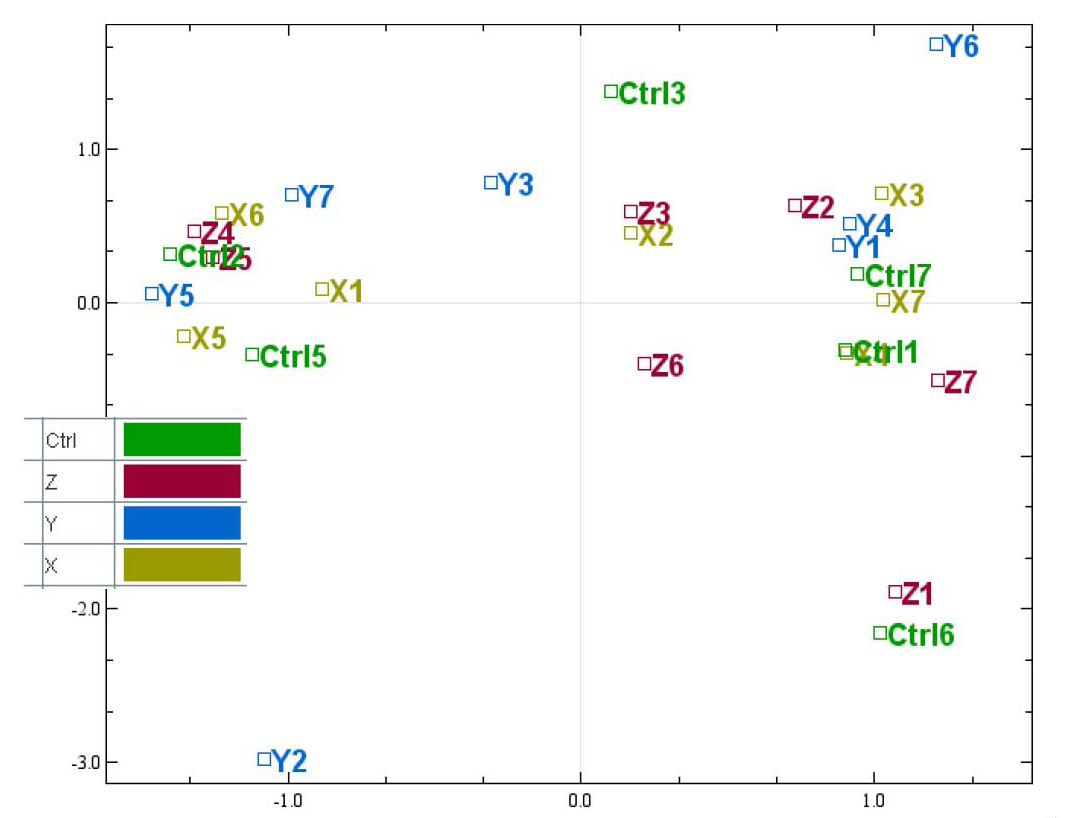However, when the plot is color coded by the technical batches of probe labeling, we see that the patterns in the data are better explained by batch than the experimental conditions.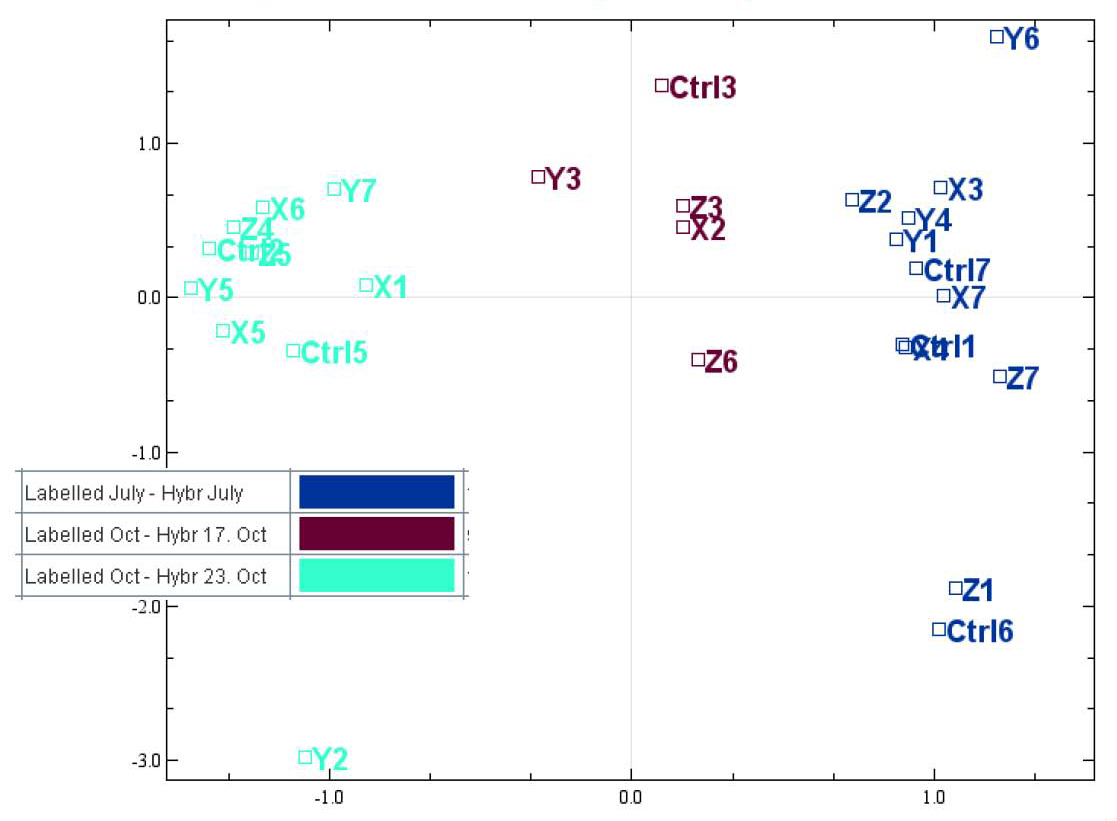

Create a PCA

We’ve already loaded the libraries we need for this module. We have also thought ahead in the previous module and created the outputs/figures and outputs/tables directories.

Below, we will plot the rlog normalized data and generate the PCA projections for the top 500 using the plotPCA function from DESeq2, specifying condition as the condition of interest, and view the simple plot generated by the function.

pca_plot = plotPCA(rld, intgroup = c('condition'), ntop = 500)
pca_plot

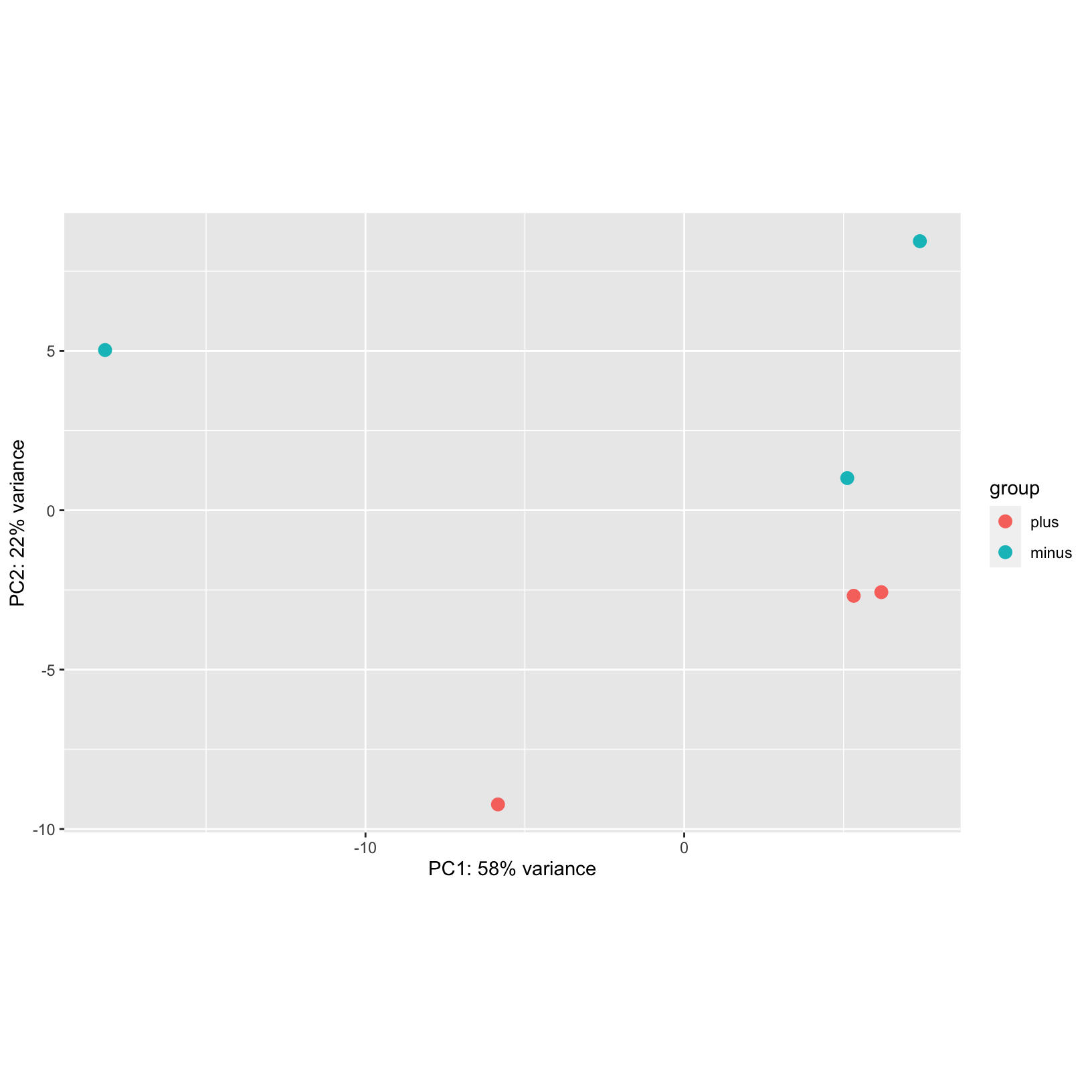
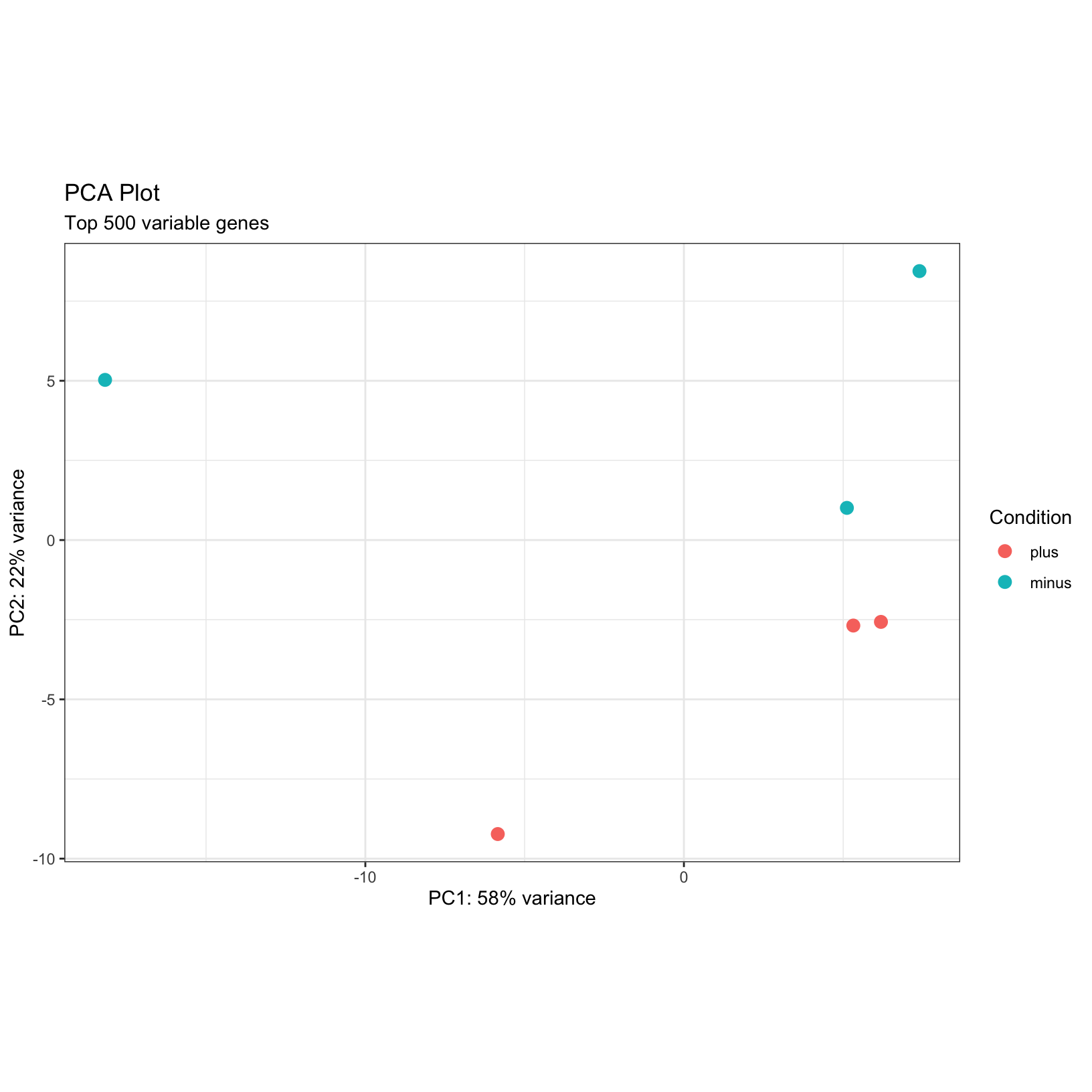
The samples don’t appear to cluster too tightly on their condition, but we do observe that they do separate in PC2. With real data, it is often the case that data doesn’t cluster as well as you’d expect, or that the covariate of interest is not associated with the first (or sometimes second or third) principal component. That doesn’t necessarily mean the experiment is a failure, but it does raise questions such as “What is associated with PC1?” Sometimes we can’t answer a question like this if we don’t have any sample phenotype to color in the PCA.

Next, let’s save this plot as a file in our outputs/figures folder. The “base R” way is to:

pdf(file = file.path('outputs', 'figures', 'PCA_rlog_condition.pdf'), width = 6, height = 6)
pca_plot
dev.off()

Alternatively, since pca_plot is a ggplot, we can use ggsave().

ggsave(
    filename = file.path('outputs', 'figures', 'PCA_rlog_condition.pdf'),
    plot = pca_plot,
    width = 6, height = 6, units = 'in')

Exercise - Customize the PCA

Since the pca_plot object is a ggplot–you can see this with class(pca_plot)–we can use what we learned at the end of the Computational Foundations Workshop to modify this plot as we might see necessary. Try doing the following to the pca_plot:

1. Add a title and subtitle to the plot using the labs() function.
2. Change the theme of the plot with theme_bw().
3. Challenge: Change the legend title to “Condition”. Hint, you can do this with the labs() function too, using the corresponding aesthetic mapping (e.g. “color”).

Remember ggplot2 adds plot components in layers, and you can add additional layers with the + sign. So if the plot already exists as an object, as pca_plot does in this case, you can add to it like pca_plot + ...

Solution

Here is one possible answer:

pca_plot +
    labs(
        title = 'PCA Plot',
        subtitle = 'Top 500 variable genes',
        color = 'Condition') +
    theme_bw()

Checkpoint: If you generated and saved the pca_plot PCA plot, please indicate with the green ‘check’ button. Otherwise, please use use the red ‘x’ button in your zoom reaction panel to have this step repeated.

Breakout Exercise 1 - Imagine a heatmap

Plotting the expression values across all samples for the top variable genes in an experiment can help to visualize how samples cluster together by their expression profiles. When combined with phenotypic data, it can help show how samples with different treatments behave relative to one another. Let’s work through this exercise in small groups and generate a heatmap of the data we’ve been working with.

Link to exercise

Download plots

Rstudio server allows us to download files through the interactive file panel on the right side. If we navigate into the plot subfolder and select the PCAplot_rlog_condition.pdf or the file, we can then click the blue gear symbol labeled More and select Export.... We should see a prompt regarding the name of the file and if we click Download the file should show up in your local “Downloads” folder.

Optional Content

Click for example code for generating a ScreePlot

A screeplot is a way to visualize the variance explained by all principal components. To generate a scree plot, the PCA results need to be used independently of plotting, such as described by this statquest post and replicated below.

# generate PCA loadings
pca = prcomp(t(assay(rld)), scale=TRUE)

## get the scree information
pca.var = pca$sdev^2
scree = pca.var/sum(pca.var)
p = barplot((scree[1:10]*100), main="Scree Plot", xlab="Principal Component", ylab="Percent Variation")

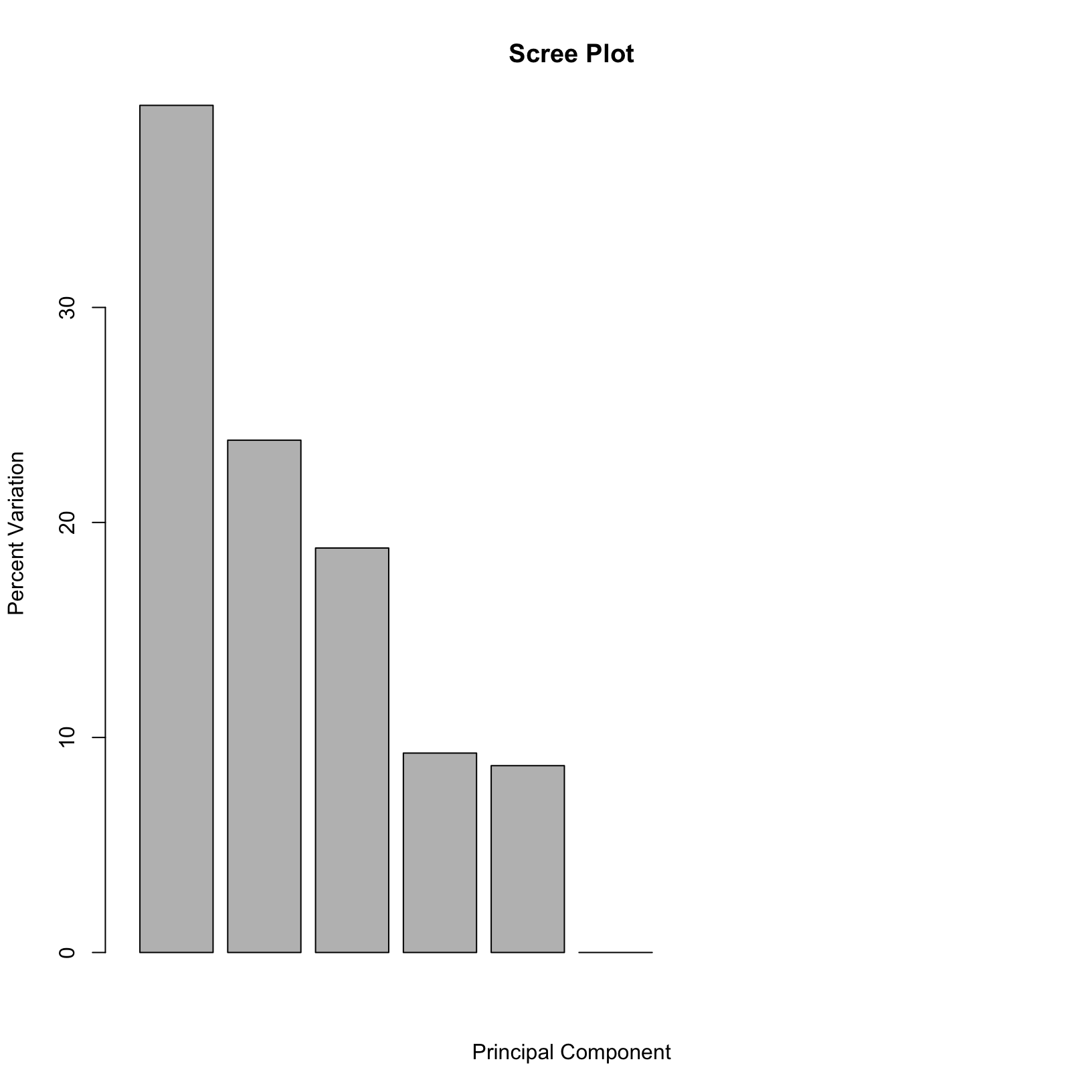
print(p)

      [,1]
 [1,]  0.7
 [2,]  1.9
 [3,]  3.1
 [4,]  4.3
 [5,]  5.5
 [6,]  6.7
 [7,]  7.9
 [8,]  9.1
 [9,] 10.3
[10,] 11.5

We can see that the majority (~65%) of the variance across our samples is explained by the first three principal components, giving us some additional confidence regarding the quality of our data. In these scree plot examples from BioTuring, the plot on the left fits what we would expect for a dataset with high signal from the experimental treatment, where the majority of the variance is explained by the first few principal components. The plot on the right illustrates a scenario where the variance is distributed across many components, which could be due to low signal from the experimental treatment, complex experimental design, or confounding factors. image: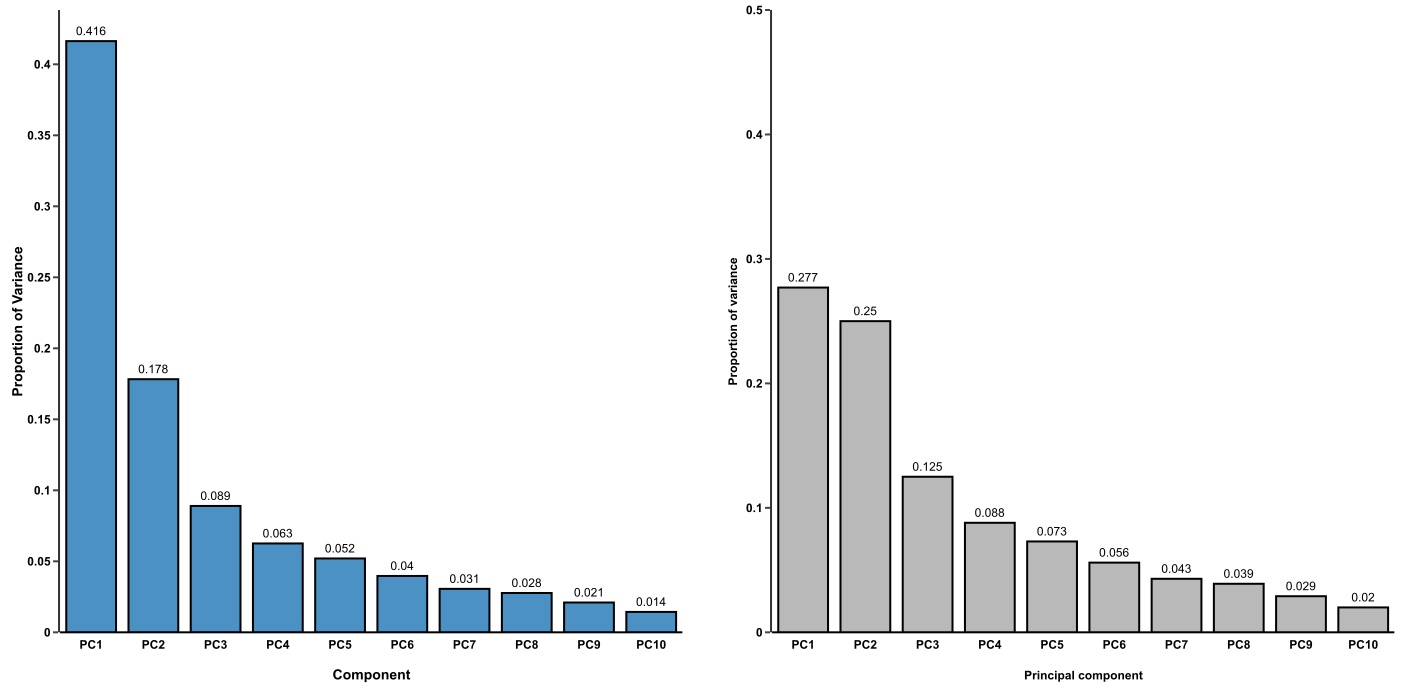

Click for code for a plot of dispersion estimates

We can visualize the dispersion estimates with the plotDispEsts function. This plot shows the the DESeq2 normalization results for our data, which centers on shrinking the variance across all genes to better fit the expected spread at a given expression level.

plotDispEsts(dds)

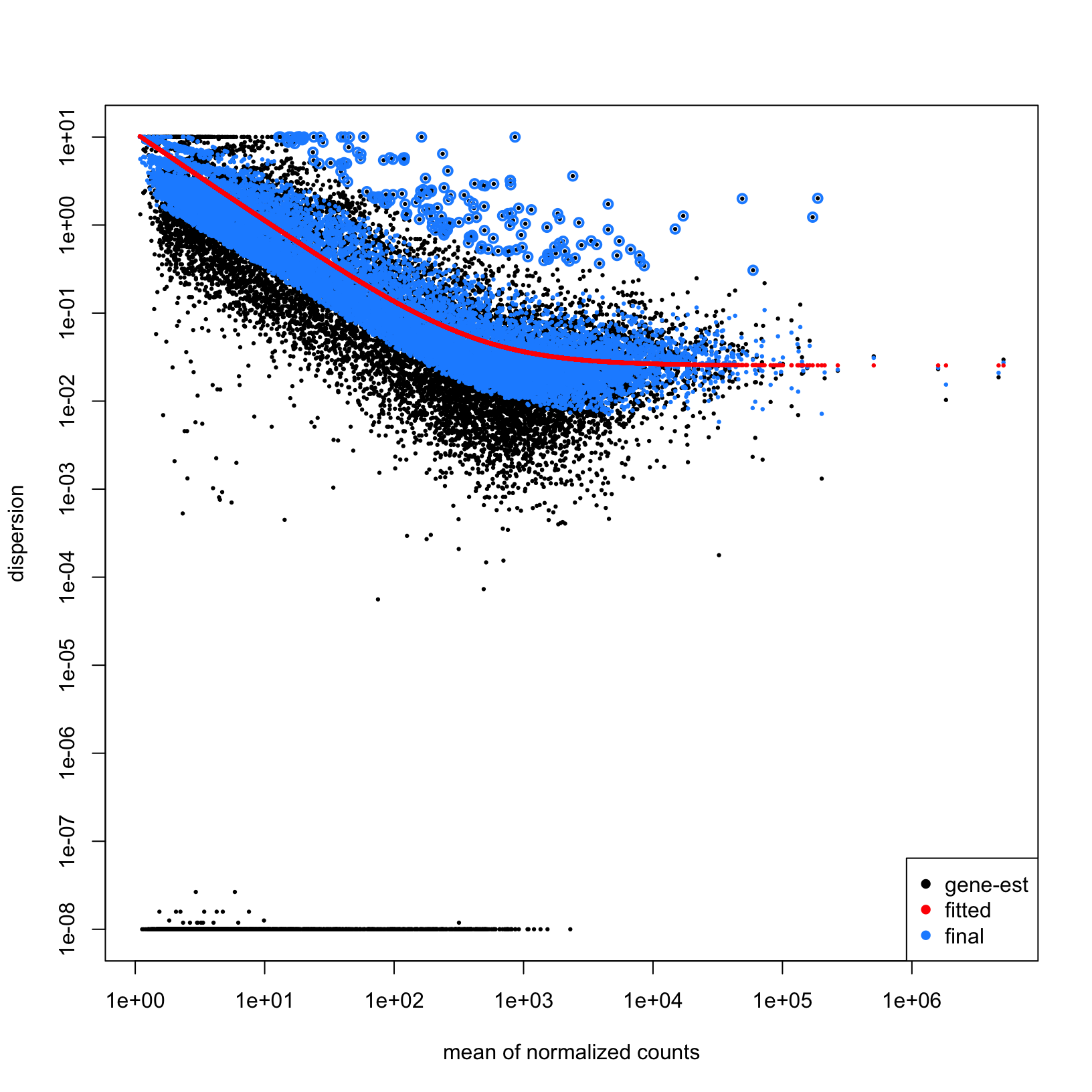Above is the raw data plotted in black, the fitted (or expected) dispersion in red, and the normalized data with scaled variance in blue. Since we have fairly small sample sizes for each condition, we see shrinkage for many genes but a reasonable correlation between the expression level and dispersions.

This HBC tutorial has a more detailed overview of estimating size factors, estimating gene dispersion, and the shrinkage procedure, as well as examples of concerning dispersion plots that may suggest reassessing quality of the experimental data.

Summary

In this section, we:

• Discussed variance within treatment groups
• Discussed technical artifacts, including batches
• Learned to generate PCA plots

---

Sources

• HBC QC tutorial: https://hbctraining.github.io/DGE_workshop/lessons/03_DGE_QC_analysis.html
• Detailed Heatmap tutorial from Galaxy: https://training.galaxyproject.org/training-material/topics/transcriptomics/tutorials/rna-seq-viz-with-heatmap2/tutorial.html
• PCA Overview: https://blog.bioturing.com/2018/06/14/principal-component-analysis-explained-simply/

---

These materials have been adapted and extended from materials listed above. These are open access materials distributed under the terms of the Creative Commons Attribution license (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.